Digital video compression and decompression algorithms (codecs) are at the heart of many modern video products, from DVD players to multimedia jukeboxes to video-capable cell phones. Understanding the operation of video compression algorithms is essential for the developers of systems, processors, and tools that target video applications. In this article, we explain the operation and characteristics of video codecs, and the demands that the codecs make on processors. We also explain how codecs differ from one another and the significance of these differences.
Starting with stills
As video clips are made of sequences of individual images, or ‘frames,’ video compression algorithms share many concepts and techniques with still image compression algorithms. Therefore, we begin our exploration of video compression by discussing the inner workings of transform-based still image compression algorithms such as JPEG, which are illustrated in figure 1.
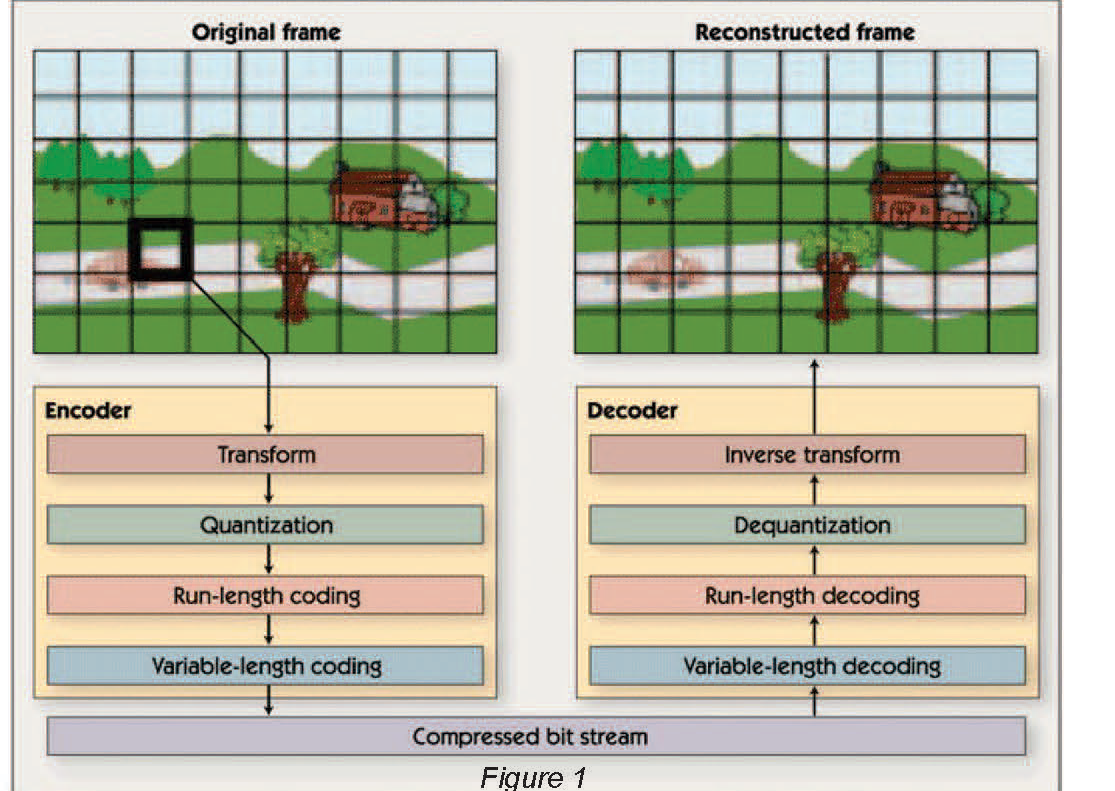
Still image compression begins by dividing the image into 8-pixel by 8-pixel blocks. The main processing steps that follow are transformation to the frequency domain, quantization of the frequency domain coefficients, run-length coding of coefficients, and variable-length coding. Still image decompression reverses these steps i.e., variable-length decoding, run-length decoding, and dequantization restores the frequent domain coefficients (with some quantization errors); and an inverse transform reconstructs the pixels in each image block from those coefficients.
The image compression techniques used in JPEG and in most video compression algorithms are ‘lossy;’ that is the original uncompressed image can’t be perfectly reconstructed from the compressed data, and some information from the original image is usually lost. The goal of using lossy compression is to minimize the number of bits that are consumed by the image while making sure that the differences between the original (uncompressed) image and the reconstructed image are not perceptible – or at least not objectionable to the human eye.
Switching to frequency
The first step in JPEG and similar image compression algorithms is to divide the image into small blocks and transform each block into a frequency-domain representation. Typically, this step uses a discrete cosine transform (DCT) on blocks that are eight pixels wide by eight pixels high. Thus, the DCT operates on 64 input pixels and yields 64 frequency domain coefficients, as shown in figure 2.
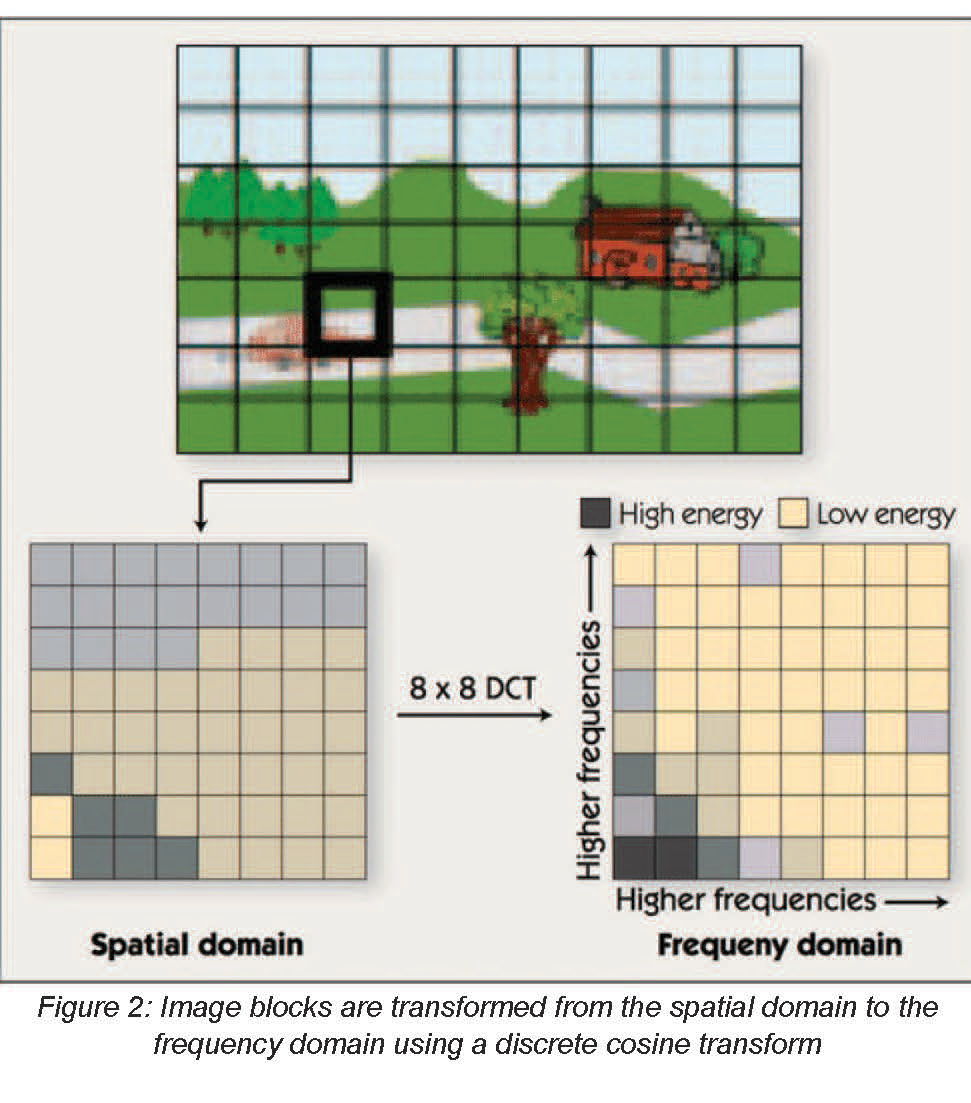
Transforms other than DCT and block sizes other than eight by eight pixels are used in some algorithms. For simplicity, we discuss only the 8×8 DCT in this article.
The DCT itself is not lossy – that is, an inverse DCT (IDCT) could be used to perfectly reconstruct the original 64 pixels from the DCT coefficients. The transform is used to facilitate frequency-based compression techniques. The human eye is more sensitive to the information contained in low frequencies (corresponding to large features in the image) than to the information contained in high frequencies (corresponding to small features). Therefore, the DCT helps separate more perceptually significant information from less perceptually significant information. After the DCT, the compression algorithm encodes the low-frequency DCT coefficients with high precision, but uses fewer bits to encode the high-frequency coefficients. In the decoding algorithm, an IDCT transforms the imperfectly coded coefficients back into an 8×8 block of pixels.
A single two-dimensional eight-by-eight DCT or IDCT requires a few hundred instruction cycles on a typical DSP such as the Texas Instruments TMS320C55x. Video compression algorithms often perform a vast number of DCTs and/ or IDCTs per second. For example, an MPEG-4 video decoder operating at VGA (640×480) resolution and a frame rate of 30 frames per second (fps) would require roughly 216,000 8×8 IDCTs per second, depending on the video content. In older video codecs these IDCT computations could consume as many as 30% of the processor cycles. In newer, more demanding codec algorithms such as H.264 however, the inverse transform (which is often a different transform than the IDCT) takes only a few percent of the decoder cycles.
Because the DCT and other transforms operate on small image blocks, the memory requirements of these functions are typically negligible compared to the size of frame buffers and other data in image and video compression applications.
Choosing the bits: Quantization & coding
After the block transform is performed, the transform coefficients for each block are compressed using quantization and coding. Quantization reduces the precision of the transform coefficients in a biased manner – more bits are used for low-frequency coefficients and fewer bits for high-frequency coefficients. This takes advantage of the fact, as noted above, that human vision is more sensitive to low-frequency information, so the high-frequency information can be more approximate. Many bits are discarded in this step. For example, a 12-bit coefficient may be rounded to the nearest of 32 predetermined values. Each of these 32 values can be represented by a five-bit symbol. In the decompression algorithm, the coefficients are ‘dequantized;’ i.e., the five-bit symbol is converted back to the 12- bit predetermined value used in the encoder. As illustrated in Figure 3, the dequantized coefficients are not equal to the original coefficients, but are close enough so that after the inverse transform is applied, the resulting image contains few or no visible artifacts.
Each frequency-domain coefficient is quantized in the encoder by rounding to the nearest of a number of pre-determined values. As this rounding discards some information, the 8×8 block of pixels reconstructed by the decoder is close – but not identical – to the corresponding block in the original image.
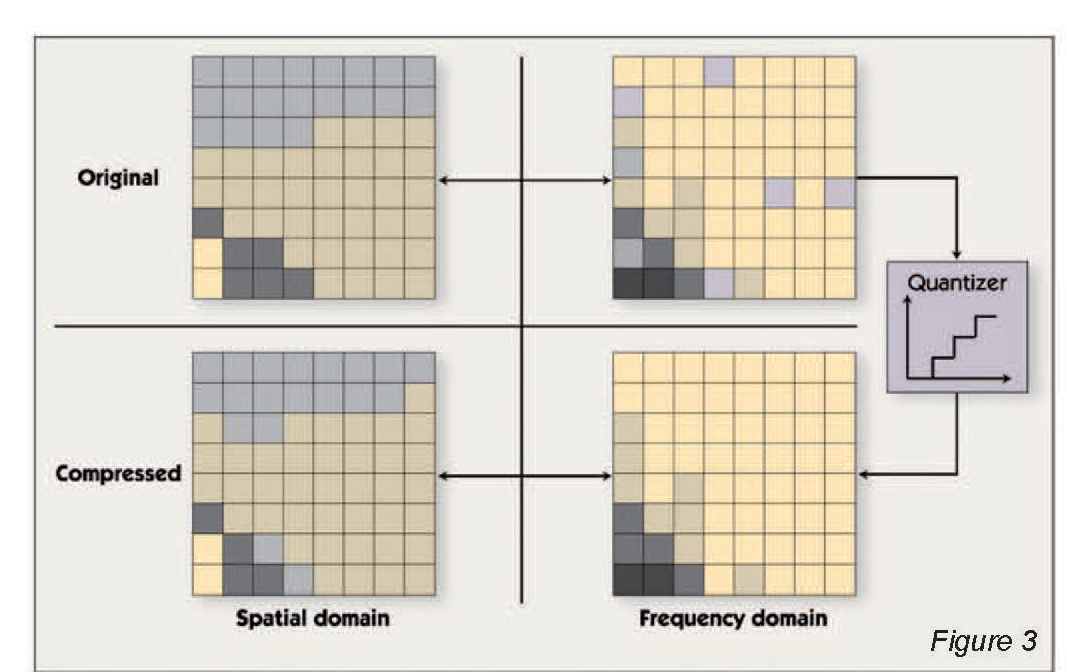
In older video algorithms, such as MPEG-2, dequantization can require anywhere from about 3% up to about 15% of the processor cycles spent in a video decoding application. Cycles spent on dequantization in modern video algorithms (such as H.264) are negligible, as are the memory requirements.
<- Previous | 1 | 2 | 3 | 4 | Next ->